
River Modeling: Blending Approaches to do More with Less
Critical infrastructure such as pipelines, transmission towers, fiber optics, and power lines face numerous and diverse threats from weather, water, and soils. As a result, they need predictive analytics to understand how infrastructure will perform relative to the risk posed by changing environmental conditions.
Knowing where infrastructure is at risk is not enough. To truly get ahead of risk, companies need to understand how infrastructure will respond to the many complex forces across changing landscapes.
By blending mapping, machine learning, and simulations, the Earthbound.ai approach enables companies to make more predictions and derive more meaningful insights about the many dimensions of risk even when data is sparse.
Blending: Mapping, Machine Learning and Simulation
Traditionally, mapping, machine learning, and simulation were covered by different disciplines. Each approach sought to understand and abstract the physical world through its own lens. Each approach is powerful, but on its own, has shortcomings.
| Mapping | Machine Learning | Simulation | |
| Defined | Representing things relative to what is nearby with polygons, lines, points, and rasters | Identifying mathematical patterns in data, using interpolation, classification, and neural nets | Predicting behaviors using physics: gravity, thermal dynamics, and fluid dynamics |
| Benefits | Useful for understanding context around events or points of interest. Some problems can be solved by leveraging spatial patterns alone | Useful for extracting and leveraging patterns in large amounts of data | Simulations are designed, using physical laws, to make predictions about complex systems |
| Shortcomings | Proximity on a map does not provide insight into how points of interest interact. | Suffers from the need for a lot of training data, lack of explanations, and from allowing predictions which violate the laws of physics | Simulations are difficult to scale without model reduction, which introduces biases. Fitting models to data is very expensive |
We built the Earthbound platform to enable users to blend these three approaches together, resulting in more accurate, explainable, and consistent results that require less data.
Stocking the Shelves with ‘Blend-able’ Models: Starting with a River Model
Over time, water accelerates infrastructure’s aging process and can even cause abrupt failure due to flooding or bank collapse. Modeling how water moves through terrain is critical for understanding where and how infrastructure will be at risk.
We are developing a feature for our platform which models rivers, a consistent tool that contains information about all the forces that can affect infrastructure: flows, depths, riverbank changes, sediment transport, and turbulence. Also, this model should generalize across all rivers. Our intent is to build a model which can be combined with other components to predict integrity issues in infrastructure such as pipelines and transmission towers. This model will sit on our platform’s virtual shelves for our users to grab and integrate with their own solutions.
We needed a model that would be informed by physics simulations in order to estimate complex phenomena like turbulence and eddies in a river. But physics simulations are computationally expensive; in order for our model to scale, we would need a method for selecting a compact domain near where we expect water to flow.
Our first step was to answer the question — where does the water belong and how does it flow?

Rivers flow downhill and meander, floods surge and subside, and turbulence churns the sediments. As water erodes landscapes, every flood, twist, turn, and meander of a river’s past and present leaves its mark on the landscape. Topography is literally a complete record of where water has been. So, to answer our question, ‘Where does water belong and how does it flow, we started our search in a map of elevation.
We also needed a way to reconstruct the body of the river itself. We needed to understand how fluctuations in depth would change its width and where the top surface of the water intersected with land at the river’s edge. USGS River gauges along the river are a great source of information about depth and flow, but this data can be sparse. Our model uses this data to represent the water’s historical and current conditions.
Modeling the river’s edge seems like it would be straightforward, but its relationship to the river is not so simple. The edge represents the boundary of a complex, dynamic hydrologic system. Fluctuations in depth change the location of the edge. Though the river’s edge is detectable with remote sensing, using satellite imagery would be a heavy way of getting at the location. To get at the relationships between depth and edge location, you would need a series of images at each location and computer vision to detect the edge of the river. All this is not necessary because these relationships are embedded in the elevation map.
One way of thinking about the river’s edge is that it represents the intersection of the top water surface and elevation. The top water surface is relatively smooth, but not at all trivial. It’s shape slopes downwards, but also curves and changes direction. To generate the river’s surface, we wanted an operator that could a) be generalized and b) handle the complex environments including dunes that come and go, floodplains, confluences, bifurcations, and the snaky-ness that can occur on many length-scales. A river centerline would not be detailed enough to represent these features.
While exploring various operators of elevation, we were surprised by how well the infinity-Laplacian identifies places where water has been flowing. We found that the infinity-Laplacian ties water movement, elevation, and sediment transport together and detects rivers moving across terrain. Therefore, we used it as an ingredient to construct an operator to generate a river surface. We know that the infinity-Laplacian is related to the theory of the optimal transport of mass (in this case, sediments) so it makes sense that it works to detect rivers. We used this operator to create an initial guess of where to add water back to our elevation map.
The infinity-Laplacian is a differential operator that is related to optimal mass transport. It provides an alternative sense of harmonic functions.
The infinity-Laplacian also has interesting implications for understanding turbulence. The operator can identify locations in the river where sediment is unstable and likely to erode. Since increased sediment transport is correlated with turbulence, we can also use this operator to find areas in the river likely to be turbulent.
The last step was to create a map of water velocities at every pixel. We built a machine learning model to compute the details of the fluid dynamics in the river channel. We constrained the model to obey the Navier-Stokes equations.
Tying it All Together
At Earthbound, we believe we can improve predictions by leveraging the interconnectedness of Earth’s systems such as water, soil, weather, and land and the laws of physics that govern these systems. In this case, we used topography to expose the past and present movement of water around the landscape. We used the infinity-Laplacian and Navier-Stokes equations as core components and constraints of this machine learning model. By blending mapping, machine learning, physics, and the prior knowledge that comes with it, we decreased the need for a lot of training data and imagery and increased the explainability of our model. Blending these approaches let us do more with less to help us understand Earth’s impacts on infrastructure integrity.
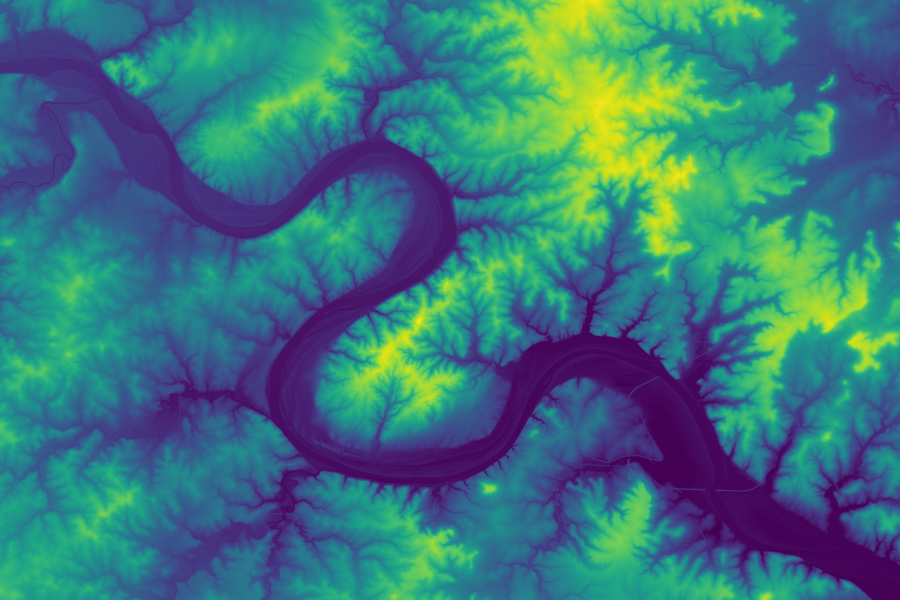
10m Elevation 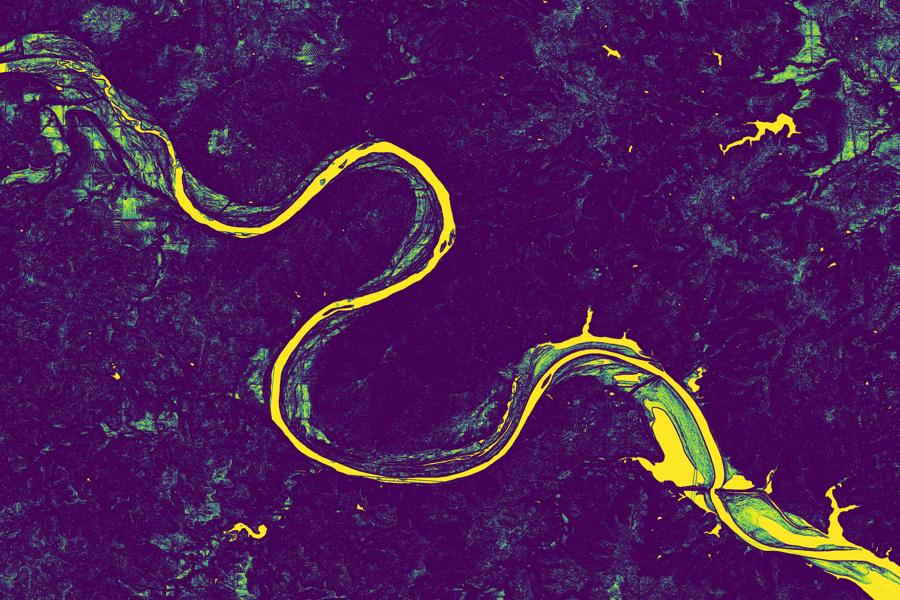
Infinity-Laplacian River Detector
What This Means for our Users
Artificial Intelligence systems are often made up of many parts such as data, models, and functions. The Earthbound platform provides users with these parts and ‘stocks the shelves’ so they can be assembled into custom solutions and deployed in a scalable compute cluster.
Now, our users can drag-and-drop these components into their own solutions to model complex interactions between critical infrastructure and soil, water, and weather.